开普勒是德国十分著名的地理学家，开普勒1609年发布椭圆定律和面积定律，在1619年发布了调和定律。椭圆定律、面积定律、调和定律这三个定律就是开普勒三大定律。开普勒三大定律是关于行星环绕太阳的静止。开普勒发现的三大定律也为牛顿万有引力定律的发现打下了根底。

1开普勒三大定律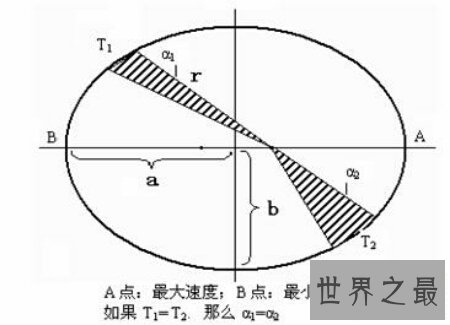

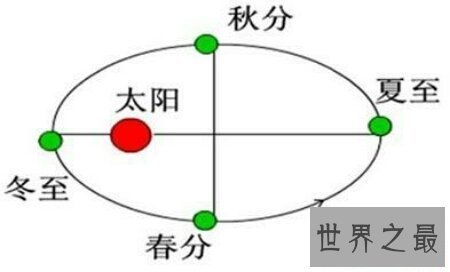
开普勒三大定律是德国地理学家开普勒提出的关于行星静止的三大定律。第一和第二定律发表于1609年，是开普勒从地理学家第谷观测火星地位所得材料中总结进去的；第三定律发表于1619年。这三大定律又分别称为椭圆定律、面积定律和调和定律。①椭圆定律一切行星绕太阳的轨道都是椭圆，太阳在椭圆的一个焦点上。

②面积定律行星和太阳的连线在相等的工夫间隔内扫过相等的面积。③调和定律一切行星绕太阳一周的恒星工夫平方与它们轨道长半轴(a i)的立方成比例。此后，学者们把第肯定律修正成为：一切行星（和彗星）的轨道都属于圆锥曲线，而太阳则在它们的一个焦点上。第二定律只内行星品质比太阳品质小得多的情况下才是精确的。假设思考到行星也吸引太阳，这便是一个二体成绩。

2定律的推导过程

开普勒三大定律用公式示意为：SAB=SCD=SEK 冗长证实：以太阳为转动轴，因为引力的切向分力为0，所以对行星的力矩为0，所以行星角动量为一恒值，而角动量又等于行星品质乘以速度和与太阳的距离，即L=mvr,其中m也是常数，故vr就是一个不变的量，而在一短工夫△t内，r扫过的面积又大约等于vr△t/2,即只与工夫无关，这就阐明了开普勒第二定律。

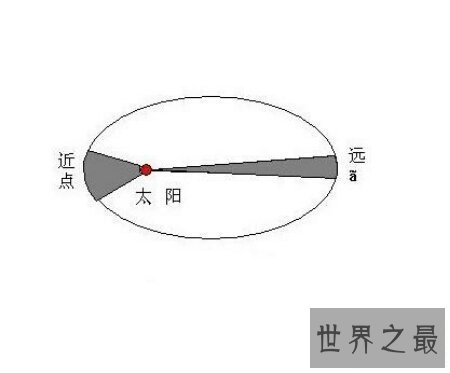
1609年，这两条定律发表在他出版的《新地理学》。 1619年，开普勒又发现了第三条定律： 开普勒第三定律（周期定律）：一切的行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等。用公式示意为：R^3/T^2=k 其中，R是行星公转轨道半长轴，T是行星公转周期，k=GM/4π^2=常数。

3开普勒定律的意义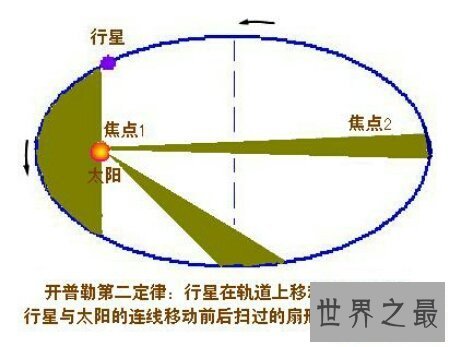

首先，开普勒三大定律在科学思维上体现出无比英勇的创造肉体。远在哥白尼创立日心宇宙体系之前，许多学者对于天动地静的观念就提出过不同见地。但对天体遵照完美的均匀圆周静止这一观念，从未有人敢疑心。开普勒却毅然否定了它。这是个十分大胆的创见。哥白尼知道几个圆合并起来就可能产生椭圆，但他素来没有用椭圆来形容过天体的轨道。

正如开普勒所说，“哥白尼没有察觉到他伸手可得的财富”。其次，开普勒定律彻底摧毁了托勒密的本轮系，把哥白尼体系从本轮的桎梏下束缚进去，为它带来充分的残缺和谨严。哥白尼丢弃古希腊人的一个先入之见，即天与地的实质差别，获得一个简略得多的体系。但它仍须用八十几个圆周来解释天体的表观静止。开普勒却找到最简略的世界体系，只用七个椭圆说就全副处理了。

4定律实用范围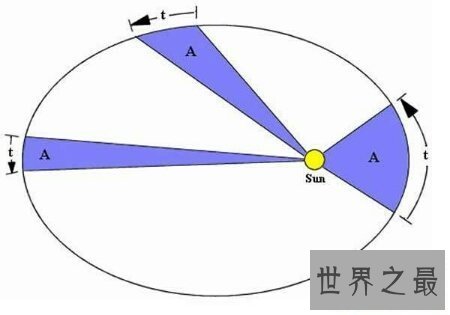

开普勒定律是一个普适定律，实用于所有二体成绩。（二体成绩就是钻研只由两个物体组成的系统的成绩，而疏忽其余物体的影响。太阳系中的任何一个行星和太阳都可能近似看作是造成了一个二体系统。）此外它还是牛顿万有引力定律的根底。实用于太阳系或类似于太阳系有行星围绕的恒星系，开普勒第三定律不实用天然卫星，由于天然卫星品质真实拧不过潮汐力的影响，以至开普勒第三定律不实用天然卫星。